Kolaps civilizací: past úspěšného začátku

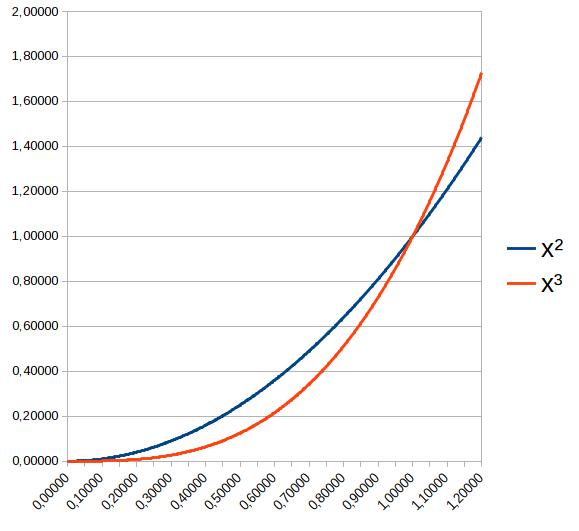
Ještě se vrátím k předchozím úvahám. Podívejme se hodně zblízka na graf z minulého článku, v němž porovnáváme růst kvadratické a kubické paraboly – tady je:

Při prvním pohledu upoutá pozornost především disproporce mezi strmostmi funkcí y=x² a y=x³. V měřítku, v němž uvedenou okolnost znázorňuje obr. 1, poněkud zaniká fakt, že v intervalu (0; 1) je tato disproporce docela dlouho právě opačná – funkce y=x³ nejdříve roste pomaleji než y=x² a změní se to až ve 2/3 intervalu. I pak je parabola kubická stále ještě pod parabolou kvadratickou, ale roste už rychleji, aby ji dohnala a předehnala v bodě 1:

Jak chování obou funkcí interpretovat v kontextu růstu systému? Domnívám se, že takto:

V počáteční fázi růstu systému disponuje jeho rozhraní kapacitou, která převyšuje jeho energetické nároky velmi zřetelně. Z grafu je vidět, že v určitém subintervalu se rozdíl mezi kapacitou rozhraní (modrá čára) a energetickými nároky systému (červená čára) dokonce ani příliš nemění a je pro růst systému příznivý – vizme např. interval <0.3;0.85>.

Prakticky to znamená, že dokud civilizace není příliš velká, může se spoléhat na to, že „zdroje jsou“, a v tom spočívá ona psychologická past:

Propustnost rozhraní v rané fázi vývoje není překážkou a daná civilizace snadno přijme představu, že příznivé okolnosti vydrží napořád. Z dosavadního průběhu věcí nemá důvod předpokládat, že by to někdy v budoucnu mohlo být jinak: budeme-li více a lépe pracovat, budeme také více a lépe růst. Doposud to tak přece vždycky bylo – proč by tomu někdy v budoucnosti mělo být jinak?

Vztah mezi rychlostí růstu povrchu a objemu tělesa však ukazuje, že všeho do času. V okamžiku, kdy si červená a modrá linka v grafu prohodí polohu, na růst zaměřená civilizace neodvratně zamíří ke kolapsu.

—ﬡ—

Nabízí se ještě jeden zajímavý pohled prostřednictvím grafu. Jak vypadá množství energie, které vzhledem k propustnosti rozhraní má systém k dispozici? Zkusme funkci y=x²-x³ , v grafu vykreslenou zeleně:

Rozdílová funkce se podle očekávání „plazí“ mezi oběma parabolami a osu x protíná v bodě 1, načež padá do záporných hodnot. Abychom chování rozdílové funkce zvýraznili, svévolně ji z estetických důvodů posílíme koeficientem n=5 takto: y=(x²-x³)*n : (V předchozím grafu bylo samozřejmě n=1)

Dokud se rozdílová funkce drží v nezáporných hodnotách, civilizace „nehladoví“, protože si prostřednictvím svého rozhraní může z okolí vzít tolik energie, kolik právě potřebuje. Z grafu lze vyčíst, že ideální podmínky ke své existenci (z hlediska energetické bilance) má civilizace v pásmu, v němž jsou všechny tři křivky téměř rovnoběžné. Ke kolapsu máme nakročeno, jakmile rozdílová funkce začne klesat. Kolaps nastává, jakmile rozdílová funkce padne do záporných hodnot.

—ﬡ—

Na úvahy o kolapsu civilizací volně navazuje další článek.